Benford’s Law for fraud detection are one of the tools used extensively by auditors and forensic accountants. With the rise in cyber crime Benford’s Law fraud detection reviews have proven an invaluable method. Due to most fraud and other transaction based crimes going unnoticed from months to years, early identification therefore is crucial. Failure to identify high risk transactions early usually has a heavy financial as well as reputation impact. Anyone processing, holding or reviewing expense data will benefit from understanding Benford’s Law and the fraud detection use. Datplan’s Benford’s law Fraud detection software allow users to quickly implement this security measure. The below article explains Benford’s Law and how company fraud and security procedures benefit.
What is Benford's Law?
Benford’s law, also known as the ‘Law of First Digits’ expects the count of the 1st digit in a number to occur a known set amount of times in a set of data. The basic principal being within any natural dataset the 1st digit of a number will start with 1 more times than a number that starts with 2. This follows, a number starting with 2 occurs more than a number starting with 3. Starting with 3 will be more often than a number starting with 4, this pattern follows to 9.
However the known ratios between numbers make using Benford’s law for fraud detection particularly useful! In a natural dataset the 1st digit should occur in the below frequency:
1 = 30.1% frequency
2 = 17.6% frequency
3 = 12.5% frequency
4 = 9.7% frequency
5 = 7.9% frequency
6 = 6.7% frequency
7 = 5.8% frequency
8 = 5.1% frequency
9 = 4.6% frequency
The distribution formula:
How is Benford's law used in Fraud Detection?
Knowing the expected 1st digit ratio means reviews can take place to check this law. If there is a deviation from this ratio it could highlight fraudulent transactions which need additional investigation.
For example if the 1st digit 4 occurred more than 9.7%, say 15% it would be worth looking at transactions starting with 4. This could happen if a manager needs to approve transactions over $500. Fraudsters may be claiming or submitting expenses just under this amount to avoid the approval process. Therefore, transactions of $4## would occur more frequently than expected.
Benford’s Law applys more than just financial data! Use in election fraud detection are amongst the ways the law has been used. This law also runs true for twitter followers, populations and distance from stars to earth in light years.
Check this site for various examples that follow Benford’s law.
Who can benefit?
Accounts Receivable: – Reviewing AR data with Benford’s law highlights invoices that could indicate fraudulent activity. Human beings think up and enter numbers that can break the natural data values expected.
Expense Claims: – Claims or expense recharges are key areas for fraud. Typically taxi receipts offer opportunity as blank templates are manually written and claimed. However if many posted claims at approximately $20 the leading digit of 2 would be over expectation and so flagged.
Bank statements:- Variable incoming and out going on bank statements can catch early fraud entries which typically start small as a test then increase in value. The start amount could be $3.50 but may be enough to tip the leading digit over expectations.
Just the 1st digit?
Expansion of the law to the second and third digit therefore allow further drill downs into the data. Third digit reviews allow increased volume management of large datasets.
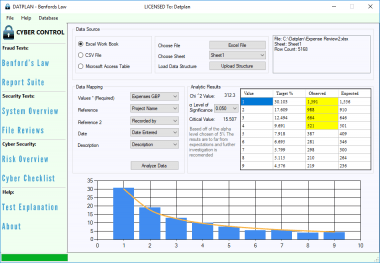
Cyber Control Software allows the mapping of company transaction data tables for quick Benford’s Law fraud testing to 3 digits.
But can variations be valid?
The frequency percentage will always deviate a number of percentage points. The number 4 may not be 9.7% but 9.9% or 9.5%, when does that variation become an issue?
A secondary test that can be run over the results and included in Cyber Control is Chi^2, or the goodness of fit test. The chi-squared test determines whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories. The formula for Chi^2:
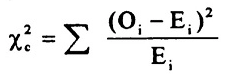
Thankfully Cyber Control includes Chi^2 reviews with variable degrees of freedom suiting the data under review.
What are the limitations of Benford's Law?
Randomly generated numbers are not naturally occurring because of this they are not measurable. Expense reports however are naturally occurring.
Other fixed numbers such as telephone numbers that all start with a standard prefix will also not conform to the rule. These are man made and so not natural datasets.
Conclusion
Benfords’s law has been proven to identify fraudulent activity in and outside of finance. Adopted by auditors and forensic accountants thus any company’s should employ this that deals in expense claims, accounts receivable and large bank transaction volumes.
Datplan created Cyber Control for this purpose. Including Chi^2 test along with an additional fraud reporting suite. Utilised by companies with a focus on staff integrity, profits and liquidity.
Datplan has been providing cyber security, fraud detection and data analysis services for over 20 years in the finance and insurance sector.